[사전학습] 3.4 데이터 변환 - 특징 생성

Posted Jan 27, 2023

By JIHWAN PARK 16 min read

3. 데이터 전처리 이해와 실무

3.1 데이터 변환 : 특징 생성

특징 생성 (Feature Creation)

원본 데이터의 조합/변환 등을 기반하여 새로운 특징들을 구축 및 생성하는 방법
=> 원본 데이터로 특징을 새롭게 생성하여 분석 과정 내 성능과 효율성 확보하고자 함
목적 및 필요성
품질 확보 : 가공을 거치지 않은 Raw 데이터 활용 기반의 모델링은 품질 확보 어려움
최적화된 형태 변환 : 효과적인 Feature를 확보하는 것이 데이터 분석 내 가장 중요한 과정임
특징 생성 방안
1. 범주 인코딩
크게 Nominal(순서가 없는)과 Ordinal(순서가 있는) 형식으로 나뉘는 범주형 변수
숫자가 아닌 범주 변수 값을 숫자로 표현하고 모델링에 적용하기 위한 과정
1. 결합 및 분해
데이터 셋의 변수들의 조합을 기반으로 새로운 특징을 구축하는 방법
변수 간의 연산 혹은 분해를 통해 새로운 특징을 구축하고 입력 변수로 모델링에 적용
1. 차원 축소
원본 데이터로부터 새로운 특징의 집합을 생성하는 것
고차원 원시 데이터 셋을 저차원으로 차원 축소하도록 새로운 특징을 생성하는 방식
1. 범주 인코딩
범주형 데이터의 알고리즘 적용을 위한 수치형 변환
One-hot Encoding
순서의 의미를 지니지 않은 범주형 변수를 처리하는 대표적 방법
k개의 범주를 지닌 범주형 변수를 k개의 변수로 변환
2-1. 결합 기반 특징 생성
변수 간의 결합을 통해 새로운 의미를 지닌 특징을 생성
Add / Divide / Subtract / Multiply
2-2. 분해 기반 특징 생성
변수의 분해를 통해 새로운 의미를 지닌 특징을 생성
특정 변수 활용 기반의 새로운 의미를 파악할 수 있는 특징을 생성하는 방법
도메인 지식 및 일반적 개념 기반으로 생성 가능 ex) 시간 -> 시간대, 요일 등..
3. 차원 축소 목적 특징 생성
3-1. 변수들이 지닌 정보를 최대한 확보하는 저차원 데이터로 생성
PCA(Principal Component Analysis)
서로 연관된 변수들이 관측되었을 때, 원본 데이터 분산 기반의 특징을 생성
주성분 간의 서로 독립을 이루도록 구성 (상관관계가 없도록 구성) 3-2. 군집 분석 기반의 고차원 데이터를 하나의 특징으로 차원 축소
Featurization via Clustering
고차원 데이터를 군집 분석을 기반으로 특징의 개수를 하나의 특징(군집 결과)으로 축소
이렇게 획득한 군집 결과 특징을 분류/회귀 등 문제 해결을 위한 입력 변수로 할용(Stacking 방법)
즉, 원본 데이터 내 여러 개의 특징을 하나의 특징으로 축소하여 모델 연산 비용 감소 추구

실습

샘플 데이터 필요

  
import numpy as np
import pandas as pd

  
data = pd.read_csv("./data/encoding_sample_data.csv", encoding='cp949')
data.head()

  
data['city'].value_counts()

1. OneHot Encoding

  
# city라는 범주형 변수 one_hot Encoding
# Pandas의 get_dummies 함수를 활용 쉽게 구혀 ㄴ가능

encoding_data = data.copy()
encoding_data = pd.get_dummies(encoding_data, columns=['city'])
encoding_data.head()

2. 결합 및 분해 기반 특징 생성

  
# 시간대 별 파악 목적
creation_data = data.copy()
creation_data.info()

  
# date 컬럼을 datetime 형식으로 변환
creation_data['date'] = pd.to_datetime(creation_data['date'])
creation_data.head()

  
creation_data.info()

  
creation_data['year'] = creation_data['date'].dt.year #연도
creation_data['month'] = creation_data['date'].dt.month #월
creation_data['day'] = creation_data['date'].dt.day #일
creation_data['hour'] = creation_data['date'].dt.hour #시간
creation_data['dayofweek'] = creation_data['date'].dt.dayofweek #요일 (월 = 0)
creation_data.head()

  
# AM PM
creation_data['ampm'] = 'AM'
creation_data.loc[creation_data['hour'] > 12, 'ampm'] = 'PM'
creation_data

3. 차원 축소 기반 특징 생성 (1) : PCA (주성분 분석)

여러 개의 변수를 지닌 고차원 데이터를 저차원으로 변환하도록 주성분들을 생성하는 알고리즘
원 변수들이 지닌 정보를 최대한 확보하는 저차원 데이터로 생성하는 방법

  
cancer = pd.read_csv('./data/wdbc.data', header=None)

# 데이터 컬럼명 지정
cancer.columns = [
    "id", "diagnosis", "radius_mean", "texture_mean", "perimeter_mean", "area_mean", "smoothness_mean", "compactness_mean", 
    "concavity_mean", "concave_points_mean", "symmetry_mean", "fractal_dimension_mean", "radius_se", "texture_se",
    "perimeter_se", "texture_worst", "smoothness_se", "compactness_se", "concavity_se", "concave_points_se", "symmetry_se",
    "fractal_dimension_se", "radius_worst", "texture_worst", "perimeter_worst", "area_worst", "smoothness_worst", "compactness_worst", 
    "concavity_worst", "concave_points_worst", "symmetry_worst", "fractal_dimension_worst"
]

# ID를 Index화
cancer = cancer.set_index('id')
cancer

	diagnosis	radius_mean	texture_mean	perimeter_mean	area_mean	smoothness_mean	compactness_mean	concavity_mean	concave_points_mean	symmetry_mean	...	radius_worst	texture_worst	perimeter_worst	area_worst	smoothness_worst	compactness_worst	concavity_worst	concave_points_worst	symmetry_worst	fractal_dimension_worst
id
842302	M	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.30010	0.14710	0.2419	...	25.380	17.33	184.60	2019.0	0.16220	0.66560	0.7119	0.2654	0.4601	0.11890
842517	M	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.08690	0.07017	0.1812	...	24.990	23.41	158.80	1956.0	0.12380	0.18660	0.2416	0.1860	0.2750	0.08902
84300903	M	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.19740	0.12790	0.2069	...	23.570	25.53	152.50	1709.0	0.14440	0.42450	0.4504	0.2430	0.3613	0.08758
84348301	M	11.42	20.38	77.58	386.1	0.14250	0.28390	0.24140	0.10520	0.2597	...	14.910	26.50	98.87	567.7	0.20980	0.86630	0.6869	0.2575	0.6638	0.17300
84358402	M	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.19800	0.10430	0.1809	...	22.540	16.67	152.20	1575.0	0.13740	0.20500	0.4000	0.1625	0.2364	0.07678
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
926424	M	21.56	22.39	142.00	1479.0	0.11100	0.11590	0.24390	0.13890	0.1726	...	25.450	26.40	166.10	2027.0	0.14100	0.21130	0.4107	0.2216	0.2060	0.07115
926682	M	20.13	28.25	131.20	1261.0	0.09780	0.10340	0.14400	0.09791	0.1752	...	23.690	38.25	155.00	1731.0	0.11660	0.19220	0.3215	0.1628	0.2572	0.06637
926954	M	16.60	28.08	108.30	858.1	0.08455	0.10230	0.09251	0.05302	0.1590	...	18.980	34.12	126.70	1124.0	0.11390	0.30940	0.3403	0.1418	0.2218	0.07820
927241	M	20.60	29.33	140.10	1265.0	0.11780	0.27700	0.35140	0.15200	0.2397	...	25.740	39.42	184.60	1821.0	0.16500	0.86810	0.9387	0.2650	0.4087	0.12400
92751	B	7.76	24.54	47.92	181.0	0.05263	0.04362	0.00000	0.00000	0.1587	...	9.456	30.37	59.16	268.6	0.08996	0.06444	0.0000	0.0000	0.2871	0.07039

569 rows × 31 columns

  
# input 및 Target 구분
input_df = cancer.drop(['diagnosis'], axis=1)
print(np.shape(input_df))

target_df = cancer[['diagnosis']]
print(np.shape(target_df))

(569, 30)
(569, 1)

  
# 30개의 독립변수로 이루어진 데이터를 주성분 분석
# 주성분 분석 수행 이전, 각 변수의 스케일이 서로 다르기 때문에 표준화 수행
from sklearn.preprocessing import StandardScaler
std_scaler = StandardScaler()

std_scaler.fit(input_df)
input_scaled = std_scaler.transform(input_df)

input_scaled

array([[ 1.09706398, -2.07333501,  1.26993369, ...,  2.29607613,
         2.75062224,  1.93701461],
       [ 1.82982061, -0.35363241,  1.68595471, ...,  1.0870843 ,
        -0.24388967,  0.28118999],
       [ 1.57988811,  0.45618695,  1.56650313, ...,  1.95500035,
         1.152255  ,  0.20139121],
       ...,
       [ 0.70228425,  2.0455738 ,  0.67267578, ...,  0.41406869,
        -1.10454895, -0.31840916],
       [ 1.83834103,  2.33645719,  1.98252415, ...,  2.28998549,
         1.91908301,  2.21963528],
       [-1.80840125,  1.22179204, -1.81438851, ..., -1.74506282,
        -0.04813821, -0.75120669]])

  
# 주성분 분석 수행
from sklearn.decomposition import PCA

# 두 개 주성분만 유지시키도록 수행
# 30개 변수의 데이터를 2개의 주성분으로 남도록 변환
pca = PCA(n_components=2)
pca.fit(input_scaled)
X_pca = pca.transform(input_scaled)
X_pca

array([[ 9.19283683,  1.94858307],
       [ 2.3878018 , -3.76817174],
       [ 5.73389628, -1.0751738 ],
       ...,
       [ 1.25617928, -1.90229671],
       [10.37479406,  1.67201011],
       [-5.4752433 , -0.67063679]])

  
# PCA 수행된 input 데이터 확인
X_pca_df = pd.DataFrame(X_pca, columns=['pc1', 'pc2'])
X_pca_df

	pc1	pc2
0	9.192837	1.948583
1	2.387802	-3.768172
2	5.733896	-1.075174
3	7.122953	10.275589
4	3.935302	-1.948072
...	...	...
564	6.439315	-3.576817
565	3.793382	-3.584048
566	1.256179	-1.902297
567	10.374794	1.672010
568	-5.475243	-0.670637

569 rows × 2 columns

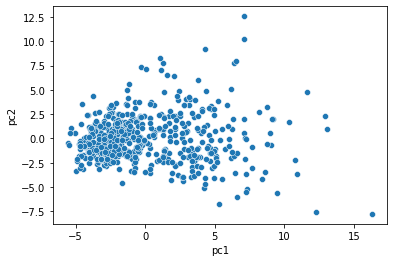
30개의 변수를 지닌 데이터가 2개의 특징들로 압축되었음

  
import matplotlib.pyplot as plt
import seaborn as sns

  
# 산점도로 2개의 주성분을 시각화
ax = sns.scatterplot(x='pc1', y='pc2', data=X_pca_df)

  
# Target과 확인을 위해 주성분 분석을 수행한 Input 데이터와 기존 Target 데이터를 Merge
target_df = target_df.reset_index()
pca_df = pd.merge(X_pca_df, target_df, left_index=True, right_index=True, how='inner')
pca_df = pca_df[['pc1', 'pc2', 'diagnosis']]
pca_df

	pc1	pc2	diagnosis
0	9.192837	1.948583	M
1	2.387802	-3.768172	M
2	5.733896	-1.075174	M
3	7.122953	10.275589	M
4	3.935302	-1.948072	M
...	...	...	...
564	6.439315	-3.576817	M
565	3.793382	-3.584048	M
566	1.256179	-1.902297	M
567	10.374794	1.672010	M
568	-5.475243	-0.670637	B

569 rows × 3 columns

  
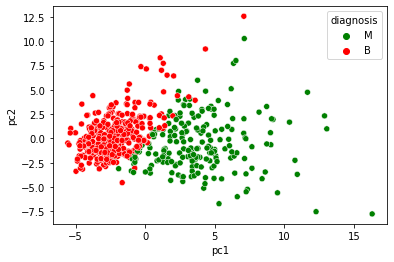
# 클래스를 색깔로 구분하여 처음 두개의 주성분으로 Target과 비교
ax = sns.scatterplot(x='pc1', y='pc2', hue='diagnosis', data=pca_df, palette=['green', 'red'])

실제 모델링에 적용하기 위해 효율적으로 활용 가능한 주성분 분석
특히, record 및 컬럼이 많은 경우 모델링 연산비용이 많이 들게 되므로 효율적인 차원 축소 기반의 특징을 생성하는 것이 분석 과정 내 필요한 과정
주성분을 선택하는 다른 방안
유지시킬 주성분 개수가 아닌 분산의 설명가능 수준을 비율로 선택 가능
- pca = PCA(n_components=0.8):
- 주성분의 수는 전체 분산의 최소 80% 수준에서 자동으로 선택
이를 통해 수치를 변경하면서 추출되는 주성분의 수 확인 가능하며, 이는 분산에 기초한 주성분 개수를 선택하는 부분에서 얼마나 많은 주성분을 사용할 것인지 확인해야 할 때 사용 가능

  
# 전체 분산의 최소 80% 수준에서 설명하는 수준의 주성분 확보
pca = PCA(n_components=0.8)
pca.fit(input_scaled)
X_pca = pca.transform(input_scaled)
X_pca_df = pd.DataFrame(X_pca)
X_pca_df

	0	1	2	3	4
0	9.192837	1.948583	-1.123166	3.633731	-1.195110
1	2.387802	-3.768172	-0.529293	1.118264	0.621775
2	5.733896	-1.075174	-0.551748	0.912083	-0.177086
3	7.122953	10.275589	-3.232790	0.152547	-2.960878
4	3.935302	-1.948072	1.389767	2.940639	0.546747
...	...	...	...	...	...
564	6.439315	-3.576817	2.459487	1.177314	-0.074824
565	3.793382	-3.584048	2.088476	-2.506028	-0.510723
566	1.256179	-1.902297	0.562731	-2.089227	1.809991
567	10.374794	1.672010	-1.877029	-2.356031	-0.033742
568	-5.475243	-0.670637	1.490443	-2.299157	-0.184703

569 rows × 5 columns

3. 차원 축소 기반 특징 생성 (2) : clustering (군집 분석)

여러 개의 변수를 하나의 변수(군집결과)로 변환 차원 축소

  
from sklearn.cluster import KMeans

  
# 일부 변수만 선택 (30개 변수 중 15개의 변수만 임의로 선정)
subset_df = input_df.iloc[:, 0:15]
subset_df

	radius_mean	texture_mean	perimeter_mean	area_mean	smoothness_mean	compactness_mean	concavity_mean	concave_points_mean	symmetry_mean	fractal_dimension_mean	radius_se	texture_se	perimeter_se	texture_worst	smoothness_se
id
842302	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.30010	0.14710	0.2419	0.07871	1.0950	0.9053	8.589	153.40	0.006399
842517	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.08690	0.07017	0.1812	0.05667	0.5435	0.7339	3.398	74.08	0.005225
84300903	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.19740	0.12790	0.2069	0.05999	0.7456	0.7869	4.585	94.03	0.006150
84348301	11.42	20.38	77.58	386.1	0.14250	0.28390	0.24140	0.10520	0.2597	0.09744	0.4956	1.1560	3.445	27.23	0.009110
84358402	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.19800	0.10430	0.1809	0.05883	0.7572	0.7813	5.438	94.44	0.011490
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
926424	21.56	22.39	142.00	1479.0	0.11100	0.11590	0.24390	0.13890	0.1726	0.05623	1.1760	1.2560	7.673	158.70	0.010300
926682	20.13	28.25	131.20	1261.0	0.09780	0.10340	0.14400	0.09791	0.1752	0.05533	0.7655	2.4630	5.203	99.04	0.005769
926954	16.60	28.08	108.30	858.1	0.08455	0.10230	0.09251	0.05302	0.1590	0.05648	0.4564	1.0750	3.425	48.55	0.005903
927241	20.60	29.33	140.10	1265.0	0.11780	0.27700	0.35140	0.15200	0.2397	0.07016	0.7260	1.5950	5.772	86.22	0.006522
92751	7.76	24.54	47.92	181.0	0.05263	0.04362	0.00000	0.00000	0.1587	0.05884	0.3857	1.4280	2.548	19.15	0.007189

569 rows × 15 columns

  
std_scaler.fit(subset_df)
subset_input_scaled = std_scaler.transform(subset_df)
subset_input_scaled

array([[ 1.09706398, -2.07333501,  1.26993369, ...,  2.83303087,
         2.48757756, -0.21400165],
       [ 1.82982061, -0.35363241,  1.68595471, ...,  0.26332697,
         0.74240195, -0.60535085],
       [ 1.57988811,  0.45618695,  1.56650313, ...,  0.8509283 ,
         1.18133606, -0.29700501],
       ...,
       [ 0.70228425,  2.0455738 ,  0.67267578, ...,  0.27669279,
         0.1806983 , -0.37934168],
       [ 1.83834103,  2.33645719,  1.98252415, ...,  1.43852964,
         1.0095027 , -0.17299998],
       [-1.80840125,  1.22179204, -1.81438851, ..., -0.15744905,
        -0.46615196,  0.04934236]])

  
# K-means 클러스터링 활용
# 군집 Label 수 설정
k = 5
model = KMeans(n_clusters=k, random_state=10)

  
model.fit(subset_input_scaled)

target_df['cluster'] = model.fit_predict(subset_input_scaled)

c:\Users\zxwlg\miniconda3\envs\dicom\lib\site-packages\sklearn\cluster\_kmeans.py:1334: UserWarning: KMeans is known to have a memory leak on Windows with MKL, when there are less chunks than available threads. You can avoid it by setting the environment variable OMP_NUM_THREADS=3.
  warnings.warn(
c:\Users\zxwlg\miniconda3\envs\dicom\lib\site-packages\sklearn\cluster\_kmeans.py:1334: UserWarning: KMeans is known to have a memory leak on Windows with MKL, when there are less chunks than available threads. You can avoid it by setting the environment variable OMP_NUM_THREADS=3.
  warnings.warn(

target_df

	index	id	diagnosis	cluster
0	0	842302	M	0
1	1	842517	M	2
2	2	84300903	M	2
3	3	84348301	M	4
4	4	84358402	M	2
...	...	...	...	...
564	564	926424	M	0
565	565	926682	M	2
566	566	926954	M	2
567	567	927241	M	0
568	568	92751	B	3

569 rows × 4 columns

  
pd.crosstab(target_df.diagnosis, target_df.cluster)

cluster	0	1	2	3	4
diagnosis
B	0	111	0	229	17
M	36	5	93	26	52

임의의 15개 변수만을 활용한 하나의 특징(군집 결과)이 Target 구분에 효과적일 것임을 예측 가능함
이처럼 많은 변수를 하나의 특징으로 구성하고, 입력 데이터의 차원을 줄인다면 모델 연산 비용 절감에 효과적

AI & 데이터분석, AIVLE SCHOOL

This post is licensed under CC BY 4.0 by the author.

3. 데이터 전처리 이해와 실무

3.1 데이터 변환 : 특징 생성

특징 생성 (Feature Creation)

목적 및 필요성

특징 생성 방안

1. 범주 인코딩

One-hot Encoding

2-1. 결합 기반 특징 생성

2-2. 분해 기반 특징 생성

3. 차원 축소 목적 특징 생성

PCA(Principal Component Analysis)

Featurization via Clustering

실습

1. OneHot Encoding

2. 결합 및 분해 기반 특징 생성

3. 차원 축소 기반 특징 생성 (1) : PCA (주성분 분석)

3. 차원 축소 기반 특징 생성 (2) : clustering (군집 분석)

Trending Tags