[사전학습] 3.5 데이터 축소 - 특징 선택

Posted Jan 27, 2023

By JIHWAN PARK 14 min read

3. 데이터 전처리 이해와 실무

3.1 데이터 축소 : 특징 선택

특징 선택 (Feature Selection)

가장 좋은 성능을 보여줄 수 있는 데이터의 부분 집합(Subset)을 찾아내는 방법
=> 모델 생성에 밀접한 데이터의 부분 집합을 선택하여 연산 효율성 및 모델 성능을 확보

목적 및 필요성

연산 효율성

특징 생성과는 다르게 원 데이터 공간 내 유의미한 특징을 선택하는 기법으로 연산 효율 및 적절한 특징을 찾기 위해 수행
원본 데이터에서 가장 유용한 특징만을 선택하여 간단한 모델 구성 및 성능을 확보하고자 하는 것이 주요 목적
특징 선택 방안
1. 필터(Filter)
특징들에 대한 통계적 점수를 부여하여 순위를 매기고 선택하는 방법론
실행 속도가 빠르다는 측면에서 시간 및 비용 측면의 장점을 보임
1) 카이제곱 필터 (Chi-square filter)
범주형인 독립 및 종속 변수 간의 유의미성을 도출하기 위한 통계적 방안
연소곃ㅇ 변수를 이산화(범주)를 하여 활용 가능
2) 상관관계 필터(Correlation filter)
연속형인 독립 및 종속변수 간 유의미성을 도출하기 위한 통계적 방안
보통 임계치(threshold) 설정하여 변수 선택

2. 래퍼(Wrapper)

특징들의 조합을 지도학습 기반 알고리즘에 반복적으로 적용하여 특징을 선택하는 방법론
최적의 데이터 조합을 찾기 때문에 성능 관점 상 유용하나 시간과 비용 크게 발생
원본 데이터 내 변수 간 조합을 탐색하여 특징 선택
반복적 특징 조합 탐색
- 원본 데이터 셋 내 변수들의 다양한 조합을 모델에 적용하는 방식
- 최적의 부분 데이터 집합(Subset)을 도출하는 방법론
- 대표적 방식으로 재귀적 특성 제거(Recursive Feature Elimination) 존재

3. 임베디드(Embedded)

모델 정확도에 기여하는 특징들을 선택하는 방법으로 Filter와 Wrpper의 장점을 결합한 방법
모델의 학습 및 생성과정에서 최적의 특징을 선택하는 방법
모델을 학습하여 정확도에 기여하는 특징을 선택하는 방안
모델 기반 특징 선택
- 알고리즘 내 자체 내장 함수로 특징을 선택하는 방식으로, 모델 성능에 기여하는 특징을 도출
- 모든 조합을 고려하고 결과를 도출하는 Wrapper 방식과 달리 학습과정에서 최적화된 변수를 선택
- 트리 계열 모델 기반의 특징 선택이 대표적(랜덤포레스트 기반 Featuer Importance 기반)

4. 특징 선택 알고리즘

랜덤포레스트 모형 기반의 알고리즘

보루타 알고리즘(Boruta Algorithm)

Boruta Algorithm은 기존 데이터 임의로 복제하여 랜덤 변수(shadow) 생성하고 원 자료와 결합하여 랜덤포레스트 모형에 적용
shadow 보다 중요도가 낮을 경우 중요하지 않은 변수로 판단 후 제거

실습

  
import numpy as np
import pandas as pd

  
cancer = pd.read_csv("./data/wdbc.data", header=None)

# 데이터 컬럼명 지정
cancer.columns = [
    "id", "diagnosis", "radius_mean", "texture_mean", "perimeter_mean", "area_mean", "smoothness_mean", "compactness_mean", 
    "concavity_mean", "concave_points_mean", "symmetry_mean", "fractal_dimension_mean", "radius_se", "texture_se",
    "perimeter_se", "texture_worst", "smoothness_se", "compactness_se", "concavity_se", "concave_points_se", "symmetry_se",
    "fractal_dimension_se", "radius_worst", "texture_worst", "perimeter_worst", "area_worst", "smoothness_worst", "compactness_worst", 
    "concavity_worst", "concave_points_worst", "symmetry_worst", "fractal_dimension_worst"
]

# ID를 Index화
cancer = cancer.set_index('id')
cancer

	diagnosis	radius_mean	texture_mean	perimeter_mean	area_mean	smoothness_mean	compactness_mean	concavity_mean	concave_points_mean	symmetry_mean	...	radius_worst	texture_worst	perimeter_worst	area_worst	smoothness_worst	compactness_worst	concavity_worst	concave_points_worst	symmetry_worst	fractal_dimension_worst
id
842302	M	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.30010	0.14710	0.2419	...	25.380	17.33	184.60	2019.0	0.16220	0.66560	0.7119	0.2654	0.4601	0.11890
842517	M	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.08690	0.07017	0.1812	...	24.990	23.41	158.80	1956.0	0.12380	0.18660	0.2416	0.1860	0.2750	0.08902
84300903	M	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.19740	0.12790	0.2069	...	23.570	25.53	152.50	1709.0	0.14440	0.42450	0.4504	0.2430	0.3613	0.08758
84348301	M	11.42	20.38	77.58	386.1	0.14250	0.28390	0.24140	0.10520	0.2597	...	14.910	26.50	98.87	567.7	0.20980	0.86630	0.6869	0.2575	0.6638	0.17300
84358402	M	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.19800	0.10430	0.1809	...	22.540	16.67	152.20	1575.0	0.13740	0.20500	0.4000	0.1625	0.2364	0.07678
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
926424	M	21.56	22.39	142.00	1479.0	0.11100	0.11590	0.24390	0.13890	0.1726	...	25.450	26.40	166.10	2027.0	0.14100	0.21130	0.4107	0.2216	0.2060	0.07115
926682	M	20.13	28.25	131.20	1261.0	0.09780	0.10340	0.14400	0.09791	0.1752	...	23.690	38.25	155.00	1731.0	0.11660	0.19220	0.3215	0.1628	0.2572	0.06637
926954	M	16.60	28.08	108.30	858.1	0.08455	0.10230	0.09251	0.05302	0.1590	...	18.980	34.12	126.70	1124.0	0.11390	0.30940	0.3403	0.1418	0.2218	0.07820
927241	M	20.60	29.33	140.10	1265.0	0.11780	0.27700	0.35140	0.15200	0.2397	...	25.740	39.42	184.60	1821.0	0.16500	0.86810	0.9387	0.2650	0.4087	0.12400
92751	B	7.76	24.54	47.92	181.0	0.05263	0.04362	0.00000	0.00000	0.1587	...	9.456	30.37	59.16	268.6	0.08996	0.06444	0.0000	0.0000	0.2871	0.07039

569 rows × 31 columns

  
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(cancer.drop(['diagnosis'], axis=1), cancer[['diagnosis']], random_state=1)
print(X_train.shape)
print(X_test.shape)

(426, 30)
(143, 30)

  
train_df = pd.merge(X_train, y_train, left_index=True, right_index=True, how='inner')
train_df

	radius_mean	texture_mean	perimeter_mean	area_mean	smoothness_mean	compactness_mean	concavity_mean	concave_points_mean	symmetry_mean	fractal_dimension_mean	...	texture_worst	perimeter_worst	area_worst	smoothness_worst	compactness_worst	concavity_worst	concave_points_worst	symmetry_worst	fractal_dimension_worst	diagnosis
id
925622	15.22	30.62	103.40	716.9	0.10480	0.20870	0.25500	0.094290	0.2128	0.07152	...	42.79	128.70	915.0	0.14170	0.79170	1.17000	0.23560	0.4089	0.14090	M
8915	14.96	19.10	97.03	687.3	0.08992	0.09823	0.05940	0.048190	0.1879	0.05852	...	26.19	109.10	809.8	0.13130	0.30300	0.18040	0.14890	0.2962	0.08472	B
848406	14.68	20.13	94.74	684.5	0.09867	0.07200	0.07395	0.052590	0.1586	0.05922	...	30.88	123.40	1138.0	0.14640	0.18710	0.29140	0.16090	0.3029	0.08216	M
922577	10.32	16.35	65.31	324.9	0.09434	0.04994	0.01012	0.005495	0.1885	0.06201	...	21.77	71.12	384.9	0.12850	0.08842	0.04384	0.02381	0.2681	0.07399	B
891703	11.85	17.46	75.54	432.7	0.08372	0.05642	0.02688	0.022800	0.1875	0.05715	...	25.75	84.35	517.8	0.13690	0.17580	0.13160	0.09140	0.3101	0.07007	B
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
866674	19.79	25.12	130.40	1192.0	0.10150	0.15890	0.25450	0.114900	0.2202	0.06113	...	33.58	148.70	1589.0	0.12750	0.38610	0.56730	0.17320	0.3305	0.08465	M
869254	10.75	14.97	68.26	355.3	0.07793	0.05139	0.02251	0.007875	0.1399	0.05688	...	20.72	77.79	441.2	0.10760	0.12230	0.09755	0.03413	0.2300	0.06769	B
859717	17.20	24.52	114.20	929.4	0.10710	0.18300	0.16920	0.079440	0.1927	0.06487	...	33.82	151.60	1681.0	0.15850	0.73940	0.65660	0.18990	0.3313	0.13390	M
88249602	14.03	21.25	89.79	603.4	0.09070	0.06945	0.01462	0.018960	0.1517	0.05835	...	30.28	98.27	715.5	0.12870	0.15130	0.06231	0.07963	0.2226	0.07617	B
854941	13.03	18.42	82.61	523.8	0.08983	0.03766	0.02562	0.029230	0.1467	0.05863	...	22.81	84.46	545.9	0.09701	0.04619	0.04833	0.05013	0.1987	0.06169	B

426 rows × 31 columns

  
import matplotlib.pyplot as plt
import seaborn as sns

  
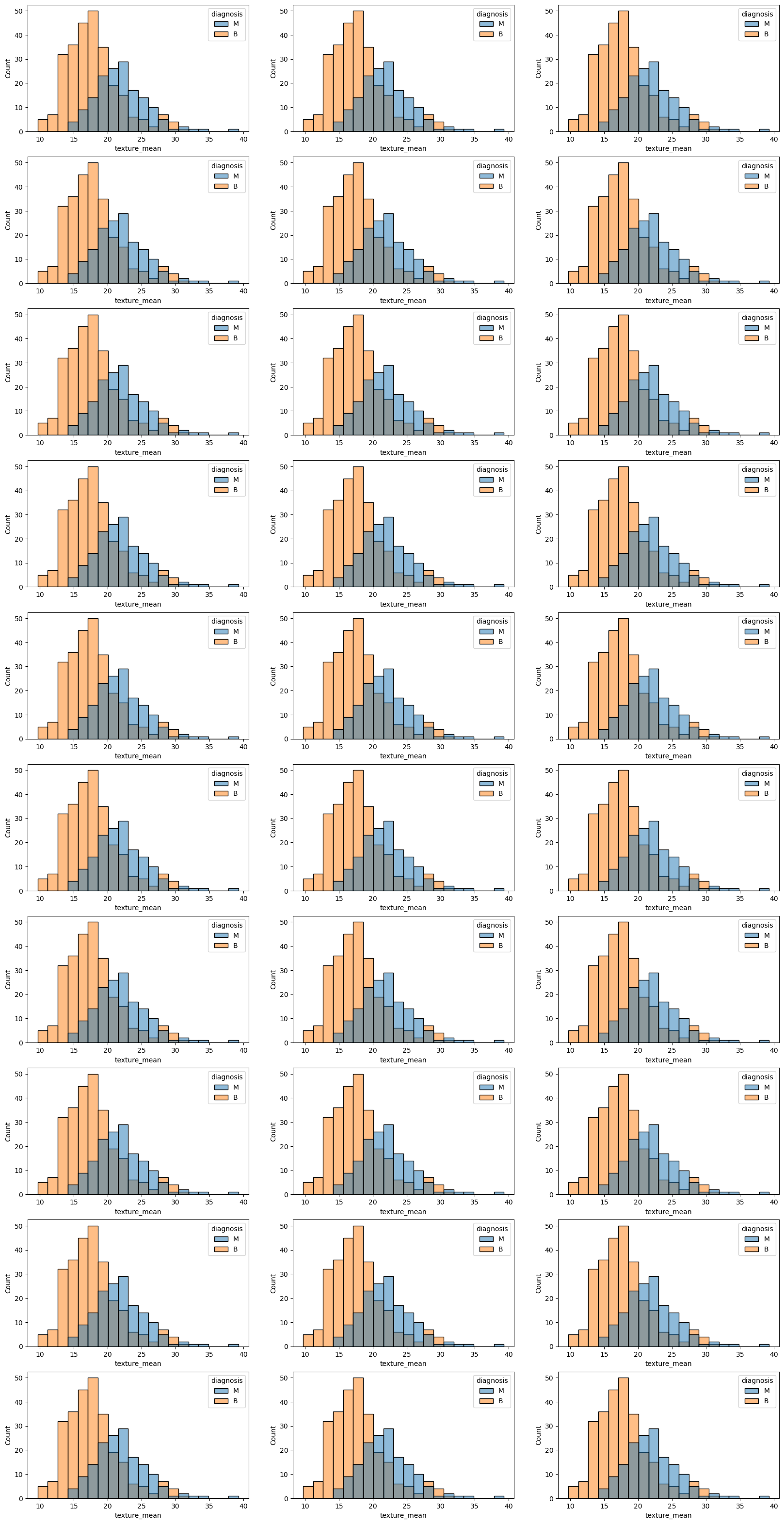
fig, axes = plt.subplots(10, 3, figsize=(20, 40))
axes = axes.flatten()

for i in range(30):
    sns.histplot(data=train_df, x=train_df.columns[1], hue='diagnosis', multiple='layer', ax=axes[i])

시각화 기반 특징들의 유의미함을 예상

유의할 것이라고 예상되는 변수
- radius_mean, perimeter_mean, area_mean, concave_point_mean, radius_worst, perimeter_worst, area_worst, concave_point_worst 등
유의하지 않을 것이라 예상되는 변수
- smoothness_mean, symmetry_mean, fractal_dimension_mean, texture_se, smoothness_se, symmetry_se, fractal_dimension_se 등
  RFE 기반 주요 특징 선택

  
from sklearn.svm import SVC
from sklearn.feature_selection import RFE

  
from sklearn.preprocessing import StandardScaler
# 스케일에 민감한 SVM의 특징에 따라 변수의 scaling을 따로 진행

scaler = StandardScaler()
scaler.fit(X_train)
scale_X_train = scaler.transform(X_train)

  
# RFE를 적용할 모델 SVM 지정
estimator_mdl = SVC(kernel="linear")
# SVM 학습 기반의 RFE 실행 및 유의미한 개수 지정 : 5개
svm_rfe = RFE(estimator=estimator_mdl, n_features_to_select=5)

svm_rfe_rst = svm_rfe.fit(scale_X_train, y_train.values.ravel())
svm_rfe_rst.ranking_
# 1로 나온 변수가 최종 유의미한 특징으로 도출된 컬럼

array([17, 23, 11, 16, 20, 25, 14,  9, 21, 13, 12, 24, 18,  1, 15, 10, 22,
        6, 26,  7,  1,  1,  2,  1, 19,  4,  3,  1,  5,  8])

  
# 도출된 특징 조합으로 test 진행
scale_X_test = scaler.transform(X_test)
prediction = pd.DataFrame(svm_rfe.predict(scale_X_test), columns=['pred_rst'])
prediction

	pred_rst
0	B
1	M
2	B
3	M
4	M
...	...
138	B
139	M
140	M
141	M
142	B

143 rows × 1 columns

  
# 타겟 클래스 데이터 수치형 변경
y_test['diagnosis'] = y_test['diagnosis'].replace('M', 1)
y_test['diagnosis'] = y_test['diagnosis'].replace('B', 0)

prediction['pred_rst'] = prediction['pred_rst'].replace('M', 1)
prediction['pred_rst'] = prediction['pred_rst'].replace('B', 0)

  
# 결과 확인
# accuracy
from sklearn.metrics import accuracy_score
print("accuracy :", round(accuracy_score(y_test['diagnosis'], prediction['pred_rst']), 5))
# auc
from sklearn.metrics import roc_auc_score
print('auc :', round(roc_auc_score(y_test['diagnosis'], prediction['pred_rst']), 5))

accuracy : 0.95105
auc : 0.94659

  
# RFE를 적용할 모델 SVM 지정
estimator_mdl = SVC(kernel="linear")
# SVM 학습 기반의 RFE 실행 및 유의미한 개수 지정 : 10개
re_svm_rfe = RFE(estimator=estimator_mdl, n_features_to_select=10)
re_svm_rfe_rst = re_svm_rfe.fit(scale_X_train, y_train.values.ravel())

re_prediction = pd.DataFrame(re_svm_rfe_rst.predict(scale_X_test), columns=['pred_rst'])

re_prediction['pred_rst'] = re_prediction['pred_rst'].replace('M', 1)
re_prediction['pred_rst'] = re_prediction['pred_rst'].replace('B', 0)

print("accuracy :", round(accuracy_score(y_test['diagnosis'], re_prediction['pred_rst']), 5))

print('auc :', round(roc_auc_score(y_test['diagnosis'], re_prediction['pred_rst']), 5))

accuracy : 0.93706
auc : 0.93523

  
chk_var = []
for name, svm_rfe_rst.ranking_ in zip(X_train.columns, svm_rfe_rst.ranking_):
    lst_chk  = [name, svm_rfe_rst.ranking_]
    chk_var.append(lst_chk)

chk_svm_rfe = pd.DataFrame(chk_var, columns = ['feature_names', 'svm_rfe_feature'])
chk_svm_rfe = chk_svm_rfe[chk_svm_rfe["svm_rfe_feature"]==1]
chk_svm_rfe

	feature_names	svm_rfe_feature
13	texture_worst	1
20	radius_worst	1
21	texture_worst	1
23	area_worst	1
27	concave_points_worst	1

Embedded 기반 특징 선택

모델 학습 성능에 기여하는 특징 선택하는 방안

  
# RF 모형 기반 특징 선택
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier

  
# RF 모형 생성
embeded_rf_selector = SelectFromModel(RandomForestClassifier(n_estimators=100, random_state=1))
embeded_rf_selector.fit(scale_X_train, y_train.values.ravel())

SelectFromModel(estimator=RandomForestClassifier(bootstrap=True, ccp_alpha=0.0,
                                                 class_weight=None,
                                                 criterion='gini',
                                                 max_depth=None,
                                                 max_features='auto',
                                                 max_leaf_nodes=None,
                                                 max_samples=None,
                                                 min_impurity_decrease=0.0,
                                                 min_impurity_split=None,
                                                 min_samples_leaf=1,
                                                 min_samples_split=2,
                                                 min_weight_fraction_leaf=0.0,
                                                 n_estimators=100, n_jobs=None,
                                                 oob_score=False,
                                                 random_state=1, verbose=0,
                                                 warm_start=False),
                max_features=None, norm_order=1, prefit=False, threshold=None)

  
# RF 기반 Embeded 특징 선택 결과
embeded_rf_support = embeded_rf_selector.get_support()
embeded_rf_feature = X_train.loc[:, embeded_rf_support].columns.tolist()
print(str(len(embeded_rf_feature)), 'selected features')

9 selected features

embeded_rf_feature

['radius_mean',
 'perimeter_mean',
 'area_mean',
 'concavity_mean',
 'concave_points_mean',
 'radius_worst',
 'perimeter_worst',
 'area_worst',
 'concave_points_worst']

Boruta Algorithm

Boruta Algorithm은 랜덤포레스트 모형 기반 특징 선택 알고리즘
기존 데이터를 임의로 복제하여 랜덤변수(shadow 변수)를 생성하고 그 보다 낮은 중요도를 지닌 특징을 제외함

  
from boruta import BorutaPy

  
# boruta 알고리즘은 랜덤포레스트 모형 기반이므로 먼저 RF 모형 설정
rf = RandomForestClassifier(random_state=1)

# boruta 기반 특징 선택
boruta_selector = BorutaPy(rf, n_estimators="auto", random_state=1)

# 'auto'인 경우는 자동으로 데이터셋 사이즈를 고려하여 자동 설정
boruta_selector.fit(scale_X_train, y_train.values.ravel())
boruta_selector.ranking_

array([1, 1, 1, 1, 1, 1, 1, 1, 3, 5, 1, 5, 1, 1, 7, 1, 1, 1, 6, 3, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 2])

  
# 최종 선택된 특징 컬럼이 어떤 컬럼인지 확인
chk_var_boruta=[]
for name, boruta_selector.ranking_ in zip(X_train.columns, boruta_selector.ranking_):
    lst_chk = [name, boruta_selector.ranking_]
    chk_var_boruta.append(lst_chk)

chk_boruta = pd.DataFrame(chk_var_boruta, columns=['feature_names', 'boruta_feature'])
chk_boruta = chk_boruta[chk_boruta["boruta_feature"]==1]
chk_boruta

	feature_names	boruta_feature
0	radius_mean	1
1	texture_mean	1
2	perimeter_mean	1
3	area_mean	1
4	smoothness_mean	1
5	compactness_mean	1
6	concavity_mean	1
7	concave_points_mean	1
10	radius_se	1
12	perimeter_se	1
13	texture_worst	1
15	compactness_se	1
16	concavity_se	1
17	concave_points_se	1
20	radius_worst	1
21	texture_worst	1
22	perimeter_worst	1
23	area_worst	1
24	smoothness_worst	1
25	compactness_worst	1
26	concavity_worst	1
27	concave_points_worst	1
28	symmetry_worst	1

  
print(np.shape(chk_boruta))

(23, 2)

  
chk_boruta = pd.DataFrame(chk_var_boruta, columns=['feature_names', 'boruta_feature'])
chk_boruta = chk_boruta[chk_boruta["boruta_feature"]!=1]
chk_boruta

	feature_names	boruta_feature
8	symmetry_mean	3
9	fractal_dimension_mean	5
11	texture_se	5
14	smoothness_se	7
18	symmetry_se	6
19	fractal_dimension_se	3
29	fractal_dimension_worst	2

AI & 데이터분석, AIVLE SCHOOL

This post is licensed under CC BY 4.0 by the author.

3. 데이터 전처리 이해와 실무

3.1 데이터 축소 : 특징 선택

특징 선택 (Feature Selection)

목적 및 필요성

특징 선택 방안

1. 필터(Filter)

1) 카이제곱 필터 (Chi-square filter)

2) 상관관계 필터(Correlation filter)