Post

[사전학습] 4.2 일변량 비시각화

Posted Updated
By JIHWAN PARK 9 min read

4.2 일변량 시각화

일변량 시각화

하나의 변수로 구성된 데이터를 전체적인 관점으로 파악할 수 있는 데이터 탐색 유형
=> 단일 변수 데이터를 다양한 그래프로 시각화하여 전체적인 관점으로 살펴보는 것이 목적

시각화 특징

시각화비시각화
- 직관적 이해 추구
- 정보 전달 시간 단축		- 효과적인 데이터 요약
- 빠른 데이터 성격 파악

범주형 시각화

1. 파이차트

  • 비율파악을 용이하게 할 수 있음
  • 시각적 전달 효과가 떨어지는 경우 : 범주 별 빈도가 유사한 경우, 범주 수가 많은 경우

    2. 막대그래프

  • 범주의 수가 많거나 범주 별 크기가 유사할 경우에 비교 수월
  • 범주 별 비교는 막대그래프 기반의 파악이 비교적 수월함

    연속형 시각화

    1. 히스토그램

  • 관측된 연속형 데이터 값들의 분포 파악 가능
  • 구간 별 분포 상태를 쉽게 알아 볼 수 있는 그래프
  • 구간 내 속하는 자료의 수가 많고 적음을 쉽게 파악
  • 막대그래프와 유사한 형태를 보유
    • 히스토그램은 연속형 변수의 빈도 분포를 표현
    • 막대그래프는 범주형 (이산형 포함) 변수의 빈도표 비교 표현

      2. 커널밀도추정

  • 관측된 연속형 데이터 값들의 분포를 분석하여 연속성 있는 확률 밀도 함수를 추정
  • 관측된 데이터로부터 변수가 가질 수 있는 모든 값의 확률(밀도)을 추정하는 것
  • 히스토그램의 한계점을 극복하기 위해 고안된 방안
    1. 구간 경계가 연속적이지 않음
    2. 구간 크기 및 시작 위치에 따라 분포가 다르게 나타남
    3. 고차원 데이터에 대한 메모리 문제 발생 가능성 존재

3. 팍스플롯

  • 연속형 데이터의 양상을 직관적으로 파악할 수 있는 방안으로 5가지 요약치를 기반으로 생성되며 다양한 정보를 손쉽게 표현
    1. 중앙값
    2. 1분위수
    3. 3분위수
    4. 최대값 (IQR Value)
    5. 최소값 (IQR Value)
  • 데이터의 개략적인 흩어짐의 형태 파악 및 IQR 기반의 이상치 판단에 용이함

실습

1
2
3
4

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

1
2
3
4
5
6

import warnings
from sklearn.datasets import load_boston
with warnings.catch_warnings():
    warnings.filterwarnings("ignore")
    data = load_boston()


1
2
3
4
5
6

X = pd.DataFrame(data.data, columns=data.feature_names)
y = pd.DataFrame(data.target, columns=['MEDV'])

housing = pd.merge(X, y, left_index=True, right_index=True, how='inner')

housing_data = housing.copy()

범주형 일변량 시각화

  • 파이차트
  • 막대그래프

    파이차트

1

housing_data.describe()
CRIMZNINDUSCHASNOXRMAGEDISRADTAXPTRATIOBLSTATMEDV
count506.000000506.000000506.000000506.000000506.000000506.000000506.000000506.000000506.000000506.000000506.000000506.000000506.000000506.000000
mean3.61352411.36363611.1367790.0691700.5546956.28463468.5749013.7950439.549407408.23715418.455534356.67403212.65306322.532806
std8.60154523.3224536.8603530.2539940.1158780.70261728.1488612.1057108.707259168.5371162.16494691.2948647.1410629.197104
min0.0063200.0000000.4600000.0000000.3850003.5610002.9000001.1296001.000000187.00000012.6000000.3200001.7300005.000000
25%0.0820450.0000005.1900000.0000000.4490005.88550045.0250002.1001754.000000279.00000017.400000375.3775006.95000017.025000
50%0.2565100.0000009.6900000.0000000.5380006.20850077.5000003.2074505.000000330.00000019.050000391.44000011.36000021.200000
75%3.67708312.50000018.1000000.0000000.6240006.62350094.0750005.18842524.000000666.00000020.200000396.22500016.95500025.000000
max88.976200100.00000027.7400001.0000000.8710008.780000100.00000012.12650024.000000711.00000022.000000396.90000037.97000050.000000
1
2
3
4

bins = [0, 20, 40, 60, 80, 100]
names = ['G1', 'G2', 'G3', 'G4', 'G5']
housing_data['AGE_G5'] = pd.cut(housing_data['AGE'], bins, labels=names)
housing_data
CRIMZNINDUSCHASNOXRMAGEDISRADTAXPTRATIOBLSTATMEDVAGE_G5
00.0063218.02.310.00.5386.57565.24.09001.0296.015.3396.904.9824.0G4
10.027310.07.070.00.4696.42178.94.96712.0242.017.8396.909.1421.6G4
20.027290.07.070.00.4697.18561.14.96712.0242.017.8392.834.0334.7G4
30.032370.02.180.00.4586.99845.86.06223.0222.018.7394.632.9433.4G3
40.069050.02.180.00.4587.14754.26.06223.0222.018.7396.905.3336.2G3
................................................
5010.062630.011.930.00.5736.59369.12.47861.0273.021.0391.999.6722.4G4
5020.045270.011.930.00.5736.12076.72.28751.0273.021.0396.909.0820.6G4
5030.060760.011.930.00.5736.97691.02.16751.0273.021.0396.905.6423.9G5
5040.109590.011.930.00.5736.79489.32.38891.0273.021.0393.456.4822.0G5
5050.047410.011.930.00.5736.03080.82.50501.0273.021.0396.907.8811.9G5

506 rows × 15 columns

1
2

pie_df_G5 = pd.DataFrame(housing_data['AGE_G5'].value_counts())
pie_df_G5
AGE_G5
G5240
G481
G376
G275
G134
1
2

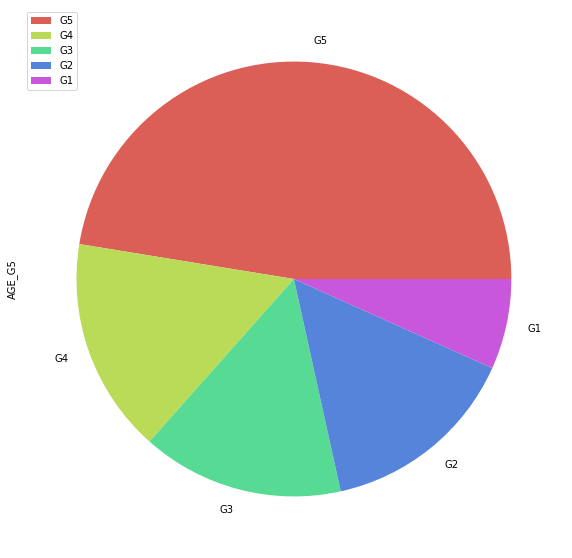
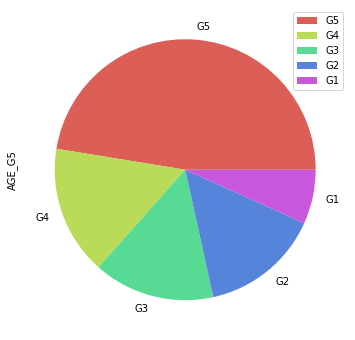
pie_df_G5.plot.pie(y='AGE_G5', figsize=(10, 10), colors=sns.color_palette('hls', len(pie_df_G5)))
plt.show()

png

1
2
3
4

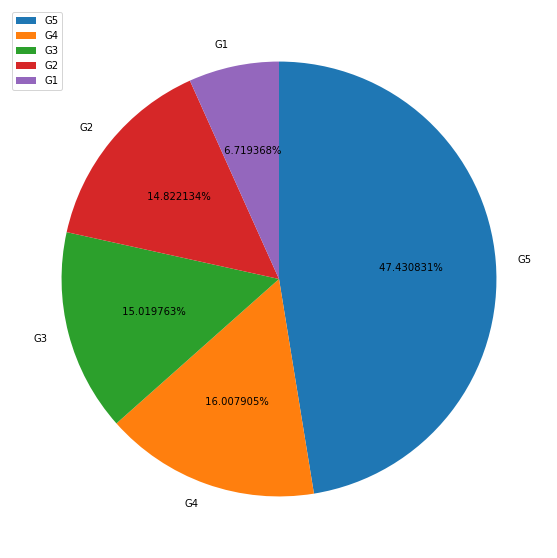
plt.figure(figsize=(10, 10))
plt.pie(pie_df_G5['AGE_G5'], labels=pie_df_G5.index, startangle=90, counterclock=False, autopct='% 2f%%')
plt.legend()
plt.show()

png

1
2
3
4
5
6
7
8

bins = list(np.linspace(0, 100, 11).astype(int))
names = ['G1', 'G2', 'G3', 'G4', 'G5', 'G6', 'G7', 'G8', 'G9', 'G10']
housing_data['AGE_G10'] = pd.cut(housing_data['AGE'], bins, labels=names)

pie_df_G10 = pd.DataFrame(housing_data['AGE_G10'].value_counts())

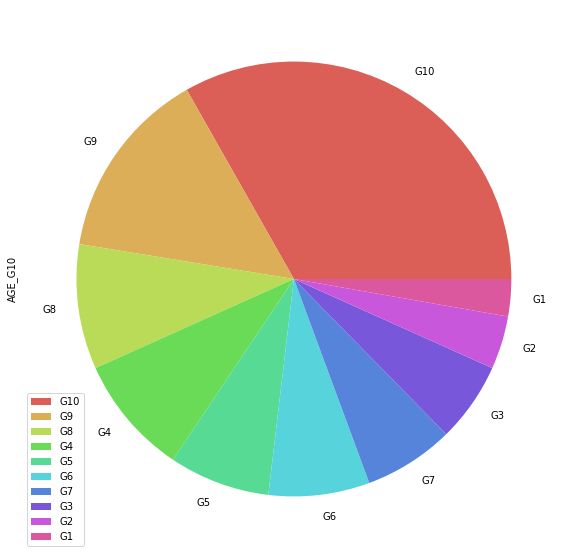
pie_df_G10.plot.pie(y='AGE_G10', figsize=(10, 10), colors=sns.color_palette('hls', len(pie_df_G10)))
plt.show()

png

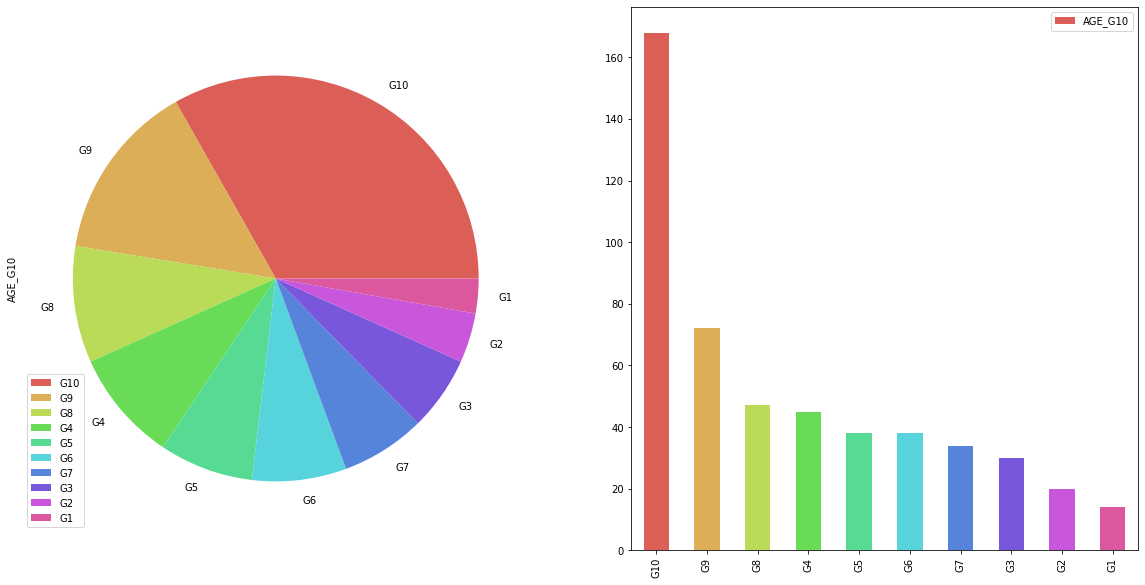
  • 5개의 범주인 경우보다, 범주 별 비교가 어려움을 보임
  • 또한, G4~G7까지 대부분 비율이 유사하게 보이므로 비교가 쉽지 않음
  • 데이터 크기가 유사할 경우, 막대그래프를 통해 크기 차이를 비교할 수 있음

    막대그래프

1
2

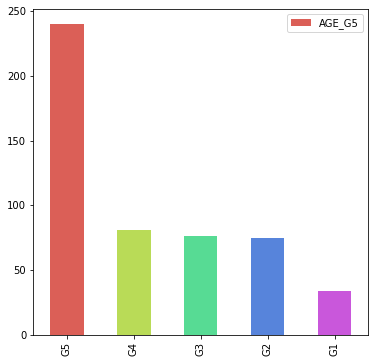
pie_df_G5.plot.bar(y='AGE_G5', figsize=(6, 6), color=sns.color_palette('hls', len(pie_df_G5)))
plt.show()

png

1
2

pie_df_G5.plot.pie(y='AGE_G5', figsize=(6, 6), colors=sns.color_palette('hls', len(pie_df_G5)))
plt.show()

png

  • G4, G3, G2의 비교가 어려운 파이차트 대비 막대그래프에서는 비교적 빈도 크기 비교가 수월함
1
2
3
4
5

fig, ax = plt.subplots(ncols=2, figsize=(20, 10))

pie_df_G10.plot.pie(y='AGE_G10', colors=sns.color_palette('hls', len(pie_df_G10)), ax=ax[0])
pie_df_G10.plot.bar(y='AGE_G10', color=sns.color_palette('hls', len(pie_df_G10)), ax=ax[1])
plt.show()

png

1

pie_df_G10
AGE_G10
G10168
G972
G847
G445
G538
G638
G734
G330
G220
G114

연속형 일변량 시각화

  • 히스토그램
  • 커널밀도그래프
  • 박스플롯

    히스토그램

1
2

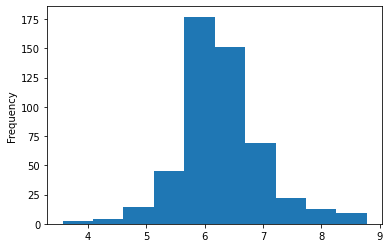
housing_data['RM'].plot.hist()
plt.show()

png

1
2

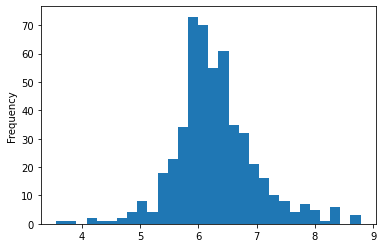
housing_data['RM'].plot.hist(bins=30)
plt.show()

png

커널밀도추정 시각화

1
2
3
4
5

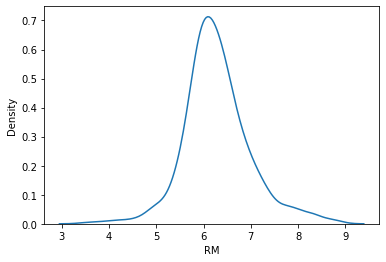
sns.kdeplot(housing_data['RM'])
plt.show()

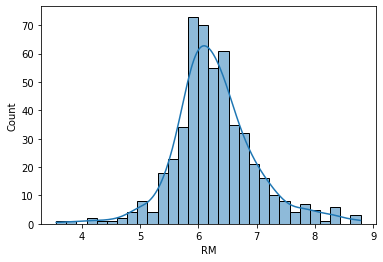
sns.histplot(housing_data['RM'], bins=30, kde=True)
plt.show()

png

png

  • 관측된 RM 변수를 기반으로 커널밀도 추정 결과의 시각화
  • 히스토그램 분포를 완만한 곡선으로 표현
1
2
3
4
5
6
7

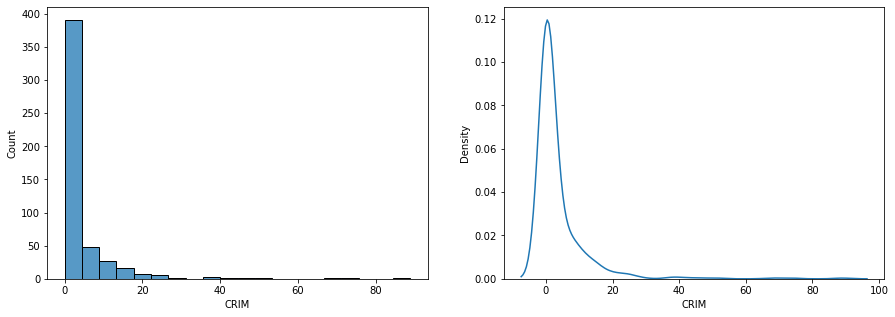
# CRIM 변수 시각화
fig, ax = plt.subplots(ncols=2, figsize=(15, 5))

sns.histplot(housing_data['CRIM'], bins=20, ax=ax[0])
sns.kdeplot(housing_data['CRIM'], ax=ax[1])

plt.show()

png

  • CRIM 컬럼의 왜도 첨도 확인 결과, 왼쪽으로 치우쳐 있고 뾰족한 모양의 분포
  • 시각화를 통해 실제 데이터 분포 형상 파악 수월

박스플롯

1
2

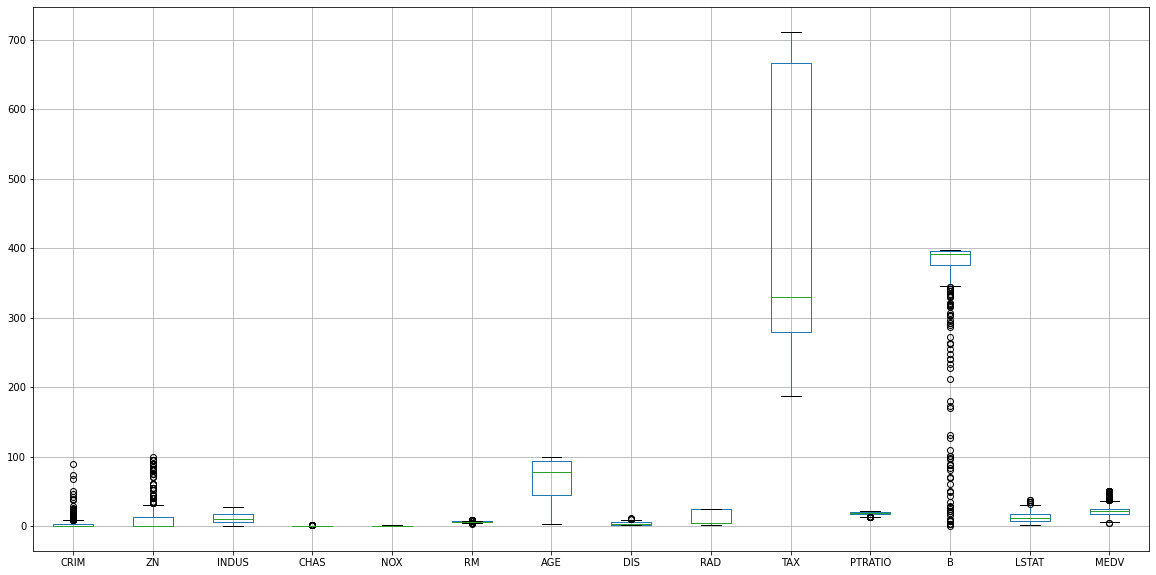
housing_data.boxplot(figsize=(20, 10))
plt.show()

png

  • 변수 별 관측치 범위가 모두 다르기 때문에, 개략적 파악 가능
  • 개별 변수 별 Box plot 시각화 필요
1
2
3
4
5
6
7
8
9

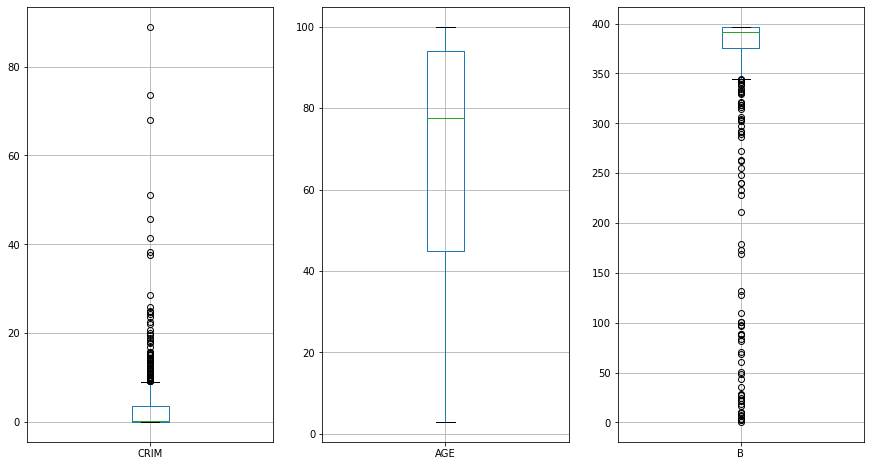
fig, ax = plt.subplots(ncols=3, figsize=(15, 8))

housing_data[['CRIM']].boxplot(ax=ax[0])
housing_data[['AGE']].boxplot(ax=ax[1])
housing_data[['B']].boxplot(ax=ax[2])

plt.show()

print(housing_data['AGE'].describe())

png

1
2
3
4
5
6
7
8
9

count    506.000000
mean      68.574901
std       28.148861
min        2.900000
25%       45.025000
50%       77.500000
75%       94.075000
max      100.000000
Name: AGE, dtype: float64

1
2
3
4
5

q1=housing_data['AGE'].quantile(0.25)
q3=housing_data['AGE'].quantile(0.75)
iqr=q3-q1
print('minimum :', q1-1.5*iqr)
print('maximum :', q3+1.5*iqr)

1
2

minimum : -28.54999999999999
maximum : 167.64999999999998
AI & 데이터분석, AIVLE SCHOOL
사전학습 AIVLE SCHOOL Python Jupyter Notebook Numpy Pandas
This post is licensed under CC BY 4.0 by the author.

[사전학습] 4.1 일변량 비시각화

[사전학습] 4.3 다변량 비시각화