Post

[사전학습] 6.2 상관분석

Posted
By JIHWAN PARK 10 min read

상관분석

상관관계

상관관계는 변수 간의 상호 관련성을 의미하며, 관계성의 정도는 통계적 또는 시각적인 방법으로 파악가능

  • 산점도
  • 상관계수 (피어슨 상관계수, 스피어맨 상관계수)

산점도 (Scatter Plot)

산점도를 이용하면 상관관계를 쉽게 파악 가능

  • 두 연속형 데이터의 관계 파악에 용이
  • 특정 관계를 갖고 있는 데이터는 한 눈에 파악 가능
  • 극단치 혹은 이상치 파악 가능
  • 한 변수의 값이 증가할 때, 다른 변수의 값도 같이 증가한다면 두 변수는 양의 상관관계
  • 한 변수는 증가하고 다른 변수는 감소한다면, 두 변수는 음의 상관관계

상관계수

두 변수 간의 함께 변화하는 경향을 객관적으로 측정할 수 있는 척도

  • 피어슨 상관계수 => 선형관계의 강도를 측정
  • 스피어맨 상관계수 비선형 순위 상관관계를 측정

    피어슨 상관계수

    두 변수 간 선형관계의 정도를 객관적으로 측정할 수 있는 방법

  • 상관계수 r은 -1부터 1까지 값을 가짐
    • r = 0 : 두 변수 간 선형관계 x
    • r = 1 : 완벽한 우상향 직선의 관계 -> 양의 상관관계
    • r = -1 : 완벽한 우하향 직선의 관계 -> 음의 상관관계

      비선형 상관계수

      변수 간 관계가 선형적이지 않다면 비선형 상관계수 또는 데이터 변환을 고려

  • 스피어맨 상관계수
    • 스피어맨은 정규분포가 아니어도 monotinic(단조) 증가/하락에 관한 비선형관계 포함 가능
  • log 변환

상관분석

측정된 두 변수 간의 선형관계가 있는지 탐색 및 확인하는 분석 방법

  • 피어슨 상관분석
    • 귀무가설
    • 대립가설
    • 검정 통계량 (t 검정)
  • 기본 가정
    • 선형성
    • 정규성
    • 등분산성

상관분석시 주의사항

상관관계 vs 인과관계

  • 상관관계가 있다고 인과관계가 있는 것은 아님
  • 인과관계가 있으면 상관관계가 있음

상관분석 Process

  1. Data 특성 파악 & 가설 설정
    • 종속변수/독립변수 : 모두 ‘등비’여야 함
    • 귀무가설 : 변수 간 선형관계 x
    • 대립가설 : 변수 간 선형관계 O
  2. 산점도를 이용한 시각화 및 가정 검토
    • 선형관계가 아니면 분석의 의미를 찾기 힘듦
    • 변수별 정규성, 등분산성 체크
  3. 목적에 맞는 분석 수행
    • Step 1 ~ 2 결과를 토대로 최종 분석 방법 선택
  4. 결과 해석 및 최종 결론 도출
    • P값 기반 상관관계 변수 선택
    • 관계의 정도 확인

실습

1
2
3
4
5
6
7
8
9

import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
import seaborn as sns

from scipy import stats # 피어슨, 스피어맨 상관계수

from sklearn.datasets import load_boston

1
2

df = pd.read_csv('./data/baseball.csv')
df

산점도를 이용한 출루율(OBP)와 타율(Bat_avg) 관계 확인

1
2

sns.scatterplot(x=df['Bat_avg'], y=df['OBP'])
plt.show()

정규성 확인

Shapiro Wilk 검정을 통해 정규성 확인

1
2

print('타율의 정규성 shapiro test : ', stats.shapiro(df['Bat_avg']))
print('출루율의 정규성 shapiro test : ', stats.shapiro(df['OBP']))

1
2

sns.histplot(df['Bat_avg'])
plt.show()

1
2

sns.histplot(df['OBP'])
plt.show()

이상치 확인

1
2

sns.pairplot(df[['Bat_avg', 'OBP', 'Num_hits']])
plt.show()

이상치 제거

1
2

new_df = df.loc[df['Num_hits'] >= 50, :].copy()
new_df

1
2

print(df.shape[0])
print(new_df.shape[0])

정규성 재검정

1
2

sns.pairplot(new_df[['Bat_avg', 'OBP']])
plt.show()

1
2

print('이상치 제거 후 타율의 정규성 shapiro test : ', stats.shapiro(new_df['Bat_avg']))
print('이상치 제거 후 출루율의 정규성 shapiro test : ', stats.shapiro(new_df['OBP']))

피어슨 상관계수 산출

1

stats.pearsonr(new_df['Bat_avg'], new_df['OBP'])

비선형 순위 상관

1

boston = load_boston()

1

type(boston)

1

sklearn.utils.Bunch

1

boston.keys()

1

dict_keys(['data', 'target', 'feature_names', 'DESCR', 'filename'])

1

print(boston.DESCR)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

.. _boston_dataset:

Boston house prices dataset
---------------------------

**Data Set Characteristics:**  

    :Number of Instances: 506 

    :Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.

    :Attribute Information (in order):
        - CRIM     per capita crime rate by town
        - ZN       proportion of residential land zoned for lots over 25,000 sq.ft.
        - INDUS    proportion of non-retail business acres per town
        - CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
        - NOX      nitric oxides concentration (parts per 10 million)
        - RM       average number of rooms per dwelling
        - AGE      proportion of owner-occupied units built prior to 1940
        - DIS      weighted distances to five Boston employment centres
        - RAD      index of accessibility to radial highways
        - TAX      full-value property-tax rate per $10,000
        - PTRATIO  pupil-teacher ratio by town
        - B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
        - LSTAT    % lower status of the population
        - MEDV     Median value of owner-occupied homes in $1000's

    :Missing Attribute Values: None

    :Creator: Harrison, D. and Rubinfeld, D.L.

This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/


This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.

The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978.   Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980.   N.B. Various transformations are used in the table on
pages 244-261 of the latter.

The Boston house-price data has been used in many machine learning papers that address regression
problems.   
     
.. topic:: References

   - Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
   - Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.

분석을 위한 데이터 프레임 구성

1
2
3

X = boston.data
boston_df = pd.DataFrame(X, columns=boston.feature_names)
display(boston_df)
CRIMZNINDUSCHASNOXRMAGEDISRADTAXPTRATIOBLSTAT
00.0063218.02.310.00.5386.57565.24.09001.0296.015.3396.904.98
10.027310.07.070.00.4696.42178.94.96712.0242.017.8396.909.14
20.027290.07.070.00.4697.18561.14.96712.0242.017.8392.834.03
30.032370.02.180.00.4586.99845.86.06223.0222.018.7394.632.94
40.069050.02.180.00.4587.14754.26.06223.0222.018.7396.905.33
..........................................
5010.062630.011.930.00.5736.59369.12.47861.0273.021.0391.999.67
5020.045270.011.930.00.5736.12076.72.28751.0273.021.0396.909.08
5030.060760.011.930.00.5736.97691.02.16751.0273.021.0396.905.64
5040.109590.011.930.00.5736.79489.32.38891.0273.021.0393.456.48
5050.047410.011.930.00.5736.03080.82.50501.0273.021.0396.907.88

506 rows × 13 columns

1
2

boston_df['MEDV'] = boston.target
boston_df
CRIMZNINDUSCHASNOXRMAGEDISRADTAXPTRATIOBLSTATMEDV
00.0063218.02.310.00.5386.57565.24.09001.0296.015.3396.904.9824.0
10.027310.07.070.00.4696.42178.94.96712.0242.017.8396.909.1421.6
20.027290.07.070.00.4697.18561.14.96712.0242.017.8392.834.0334.7
30.032370.02.180.00.4586.99845.86.06223.0222.018.7394.632.9433.4
40.069050.02.180.00.4587.14754.26.06223.0222.018.7396.905.3336.2
.............................................
5010.062630.011.930.00.5736.59369.12.47861.0273.021.0391.999.6722.4
5020.045270.011.930.00.5736.12076.72.28751.0273.021.0396.909.0820.6
5030.060760.011.930.00.5736.97691.02.16751.0273.021.0396.905.6423.9
5040.109590.011.930.00.5736.79489.32.38891.0273.021.0393.456.4822.0
5050.047410.011.930.00.5736.03080.82.50501.0273.021.0396.907.8811.9

506 rows × 14 columns

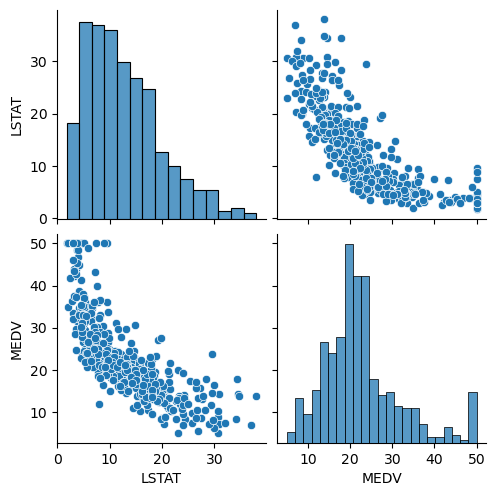
특정 지역 하위계층의 비율을 나타내는 LSTAT과 해당 지역 집값(중앙값)을 나타내는 MEDV 관계 확인

1
2

sns.pairplot(boston_df[['LSTAT', 'MEDV']])
plt.show()

png

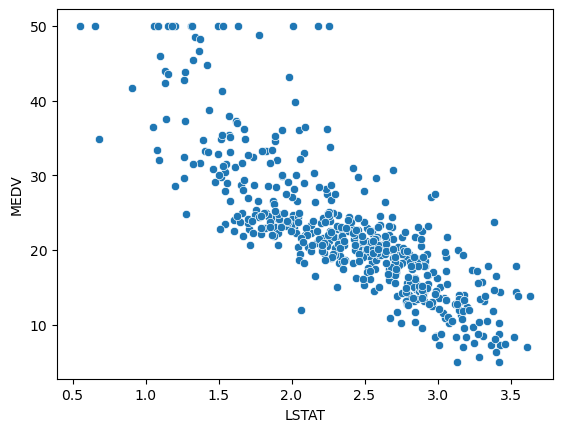
Log 변환

1
2

sns.scatterplot(x=np.log(boston_df['LSTAT']), y=boston_df['MEDV'])
plt.show()

png

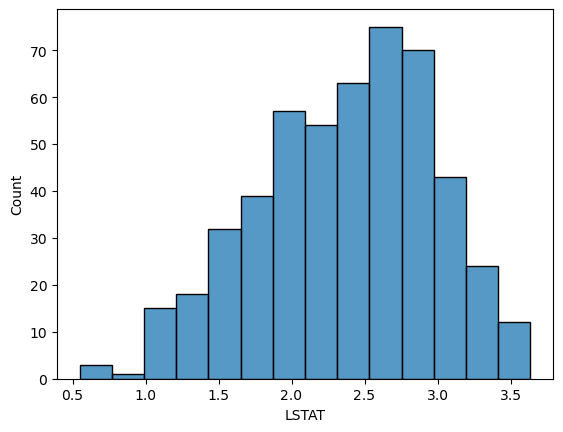
1
2

sns.histplot(np.log(boston_df['LSTAT']))
plt.show()

png

1

stats.shapiro(np.log(boston_df['LSTAT']))

1

ShapiroResult(statistic=0.9861650466918945, pvalue=9.793916979106143e-05)

비선형 순위 상관 스피어맨

1

stats.spearmanr(boston_df['LSTAT'], boston_df['MEDV'])

1

SpearmanrResult(correlation=-0.8529141394922163, pvalue=2.221727524313283e-144)

1

  AI & 데이터분석, AIVLE SCHOOL
  사전학습 AIVLE SCHOOL Python Jupyter Notebook Numpy Pandas
 This post is licensed under  CC BY 4.0  by the author.
 
[사전학습] 6.1 가설의 의의와 검정
 
[사전학습] 6.3 회귀분석